Get Early Bird Offer In Your CAT 2025 Preparation
CALL NOW +91 83060 56876cat 2023 Complete Paper Solution | DILR Slot 3
Question Palette
Question 1.

There are only three female students – Amala, Koli and Rini – and only three male students – Biman, Mathew and Shyamal – in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
There are only three female students – Amala, Koli and Rini – and only three male students – Biman, Mathew and Shyamal – in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
What was Rini's score in the project?
Question 2.

There are only three female students – Amala, Koli and Rini – and only three male students – Biman, Mathew and Shyamal – in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
There are only three female students – Amala, Koli and Rini – and only three male students – Biman, Mathew and Shyamal – in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
What was the weight of the test component?
Question 3.

There are only three female students – Amala, Koli and Rini – and only three male students – Biman, Mathew and Shyamal – in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
There are only three female students – Amala, Koli and Rini – and only three male students – Biman, Mathew and Shyamal – in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
What was the maximum aggregate score obtained by the students?
Question 4.

There are only three female students – Amala, Koli and Rini – and only three male students – Biman, Mathew and Shyamal – in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
There are only three female students – Amala, Koli and Rini – and only three male students – Biman, Mathew and Shyamal – in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
What was Mathew's score in the test?
Question 5.

There are only three female students – Amala, Koli and Rini – and only three male students – Biman, Mathew and Shyamal – in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
Which of the following pairs of students were part of the same project team?
i) Amala and Biman
ii) Koli and Mathew
There are only three female students – Amala, Koli and Rini – and only three male students – Biman, Mathew and Shyamal – in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1.
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60, respectively.
2. The test scores of the students were all multiples of 10; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
Which of the following pairs of students were part of the same project team?
i) Amala and Biman
ii) Koli and Mathew
Question 6.

In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months – January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.

In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months – January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.
What was the total number of registrations in April?
Question 7.

In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months – January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.

In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months – January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.
What was the number of online registrations in January?
Question 8.

In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months – January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.

Which of the following statements can be true?
I. The number of offline registrations was the smallest in May.
II. The total number of registrations was the smallest in February.
In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months – January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.
Which of the following statements can be true?
I. The number of offline registrations was the smallest in May.
II. The total number of registrations was the smallest in February.
Question 9.

In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months – January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.

In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months – January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.
What best can be concluded about the number of offline registrations in February?
Question 10.

In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months – January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.

Which pair of months definitely had the same total number of registrations?
I. January and April
II. February and May
In a coaching class, some students register online, and some others register offline. No student registers both online and offline; hence the total registration number is the sum of online and offline registrations. The following facts and table pertain to these registration numbers for the five months – January to May of 2023. The table shows the minimum, maximum, median registration numbers of these five months, separately for online, offline and total number of registrations. The following additional facts are known.
1. In every month, both online and offline registration numbers were multiples of 10.
2. In January, the number of offline registrations was twice that of online registrations.
3. In April, the number of online registrations was twice that of offline registrations.
4. The number of online registrations in March was the same as the number of offline registrations in February.
5. The number of online registrations was the largest in May.
Which pair of months definitely had the same total number of registrations?
I. January and April
II. February and May
Question 11.

An air conditioner (AC) company has four dealers – D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs – Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known: 1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs. 3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
An air conditioner (AC) company has four dealers – D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs – Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known: 1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs. 3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
How many Split Inverter ACs did D2 sell?
Question 12.

An air conditioner (AC) company has four dealers – D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs – Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known: 1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs. 3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
An air conditioner (AC) company has four dealers – D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs – Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known: 1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs. 3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
What percentage of ACs sold were of Non-inverter type?
Question 13.

An air conditioner (AC) company has four dealers – D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs – Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known: 1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs. 3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
An air conditioner (AC) company has four dealers – D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs – Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known: 1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs. 3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
What was the total number of ACs sold by D2 and D4?
Question 14.

An air conditioner (AC) company has four dealers – D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs – Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known: 1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs. 3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
An air conditioner (AC) company has four dealers – D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs – Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known: 1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs. 3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
Which of the following statements is necessarily false?
Question 15.

An air conditioner (AC) company has four dealers – D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs – Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known: 1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs. 3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
An air conditioner (AC) company has four dealers – D1, D2, D3 and D4 in a city. It is evaluating sales performances of these dealers. The company sells two variants of ACs – Window and Split. Both these variants can be either Inverter type or Non-inverter type. It is known that of the total number of ACs sold in the city, 25% were of Window variant, while the rest were of Split variant. Among the Inverter ACs sold, 20% were of Window variant.
The following information is also known: 1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs. 3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city.4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it.5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.6. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
7. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2.
If D3 and D4 sold an equal number of ACs, then what was the number of Non-inverter ACs sold by D2?
Question 16.

A, B, C, D, E and F are the six police stations in an area, which are connected by streets as shown below. Four teams – Team 1, Team 2, Team 3 and Team 4 –
patrol these streets continuously between 09:00 hrs. and 12:00 hrs. each day.
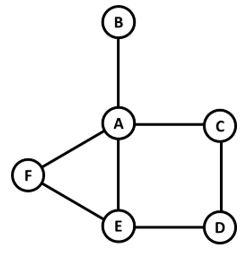
The teams need 30 minutes to cross a street connecting one police station to another. All four teams start from Station A at 09:00 hrs. and must return to Station A by 12:00 hrs. They can also pass via Station A at any point on their journeys.
The following facts are known.
1. None of the streets has more than one team traveling along it in any direction at any point in time.
2. Teams 2 and 3 are the only ones in stations E and D respectively at 10:00 hrs.
3. Teams 1 and 3 are the only ones in station E at 10:30 hrs.
4. Teams 1 and 4 are the only ones in stations B and E respectively at 11:30 hrs.
5. Team 1 and Team 4 are the only teams that patrol the street connecting stations A and E.
6. Team 4 never passes through Stations B, D or F.
A, B, C, D, E and F are the six police stations in an area, which are connected by streets as shown below. Four teams – Team 1, Team 2, Team 3 and Team 4 –
patrol these streets continuously between 09:00 hrs. and 12:00 hrs. each day.
The teams need 30 minutes to cross a street connecting one police station to another. All four teams start from Station A at 09:00 hrs. and must return to Station A by 12:00 hrs. They can also pass via Station A at any point on their journeys.
The following facts are known.
1. None of the streets has more than one team traveling along it in any direction at any point in time.
2. Teams 2 and 3 are the only ones in stations E and D respectively at 10:00 hrs.
3. Teams 1 and 3 are the only ones in station E at 10:30 hrs.
4. Teams 1 and 4 are the only ones in stations B and E respectively at 11:30 hrs.
5. Team 1 and Team 4 are the only teams that patrol the street connecting stations A and E.
6. Team 4 never passes through Stations B, D or F.
Which one among the following stations is visited the largest number of times?
Question 17.

A, B, C, D, E and F are the six police stations in an area, which are connected by streets as shown below. Four teams – Team 1, Team 2, Team 3 and Team 4 –
patrol these streets continuously between 09:00 hrs. and 12:00 hrs. each day.

The teams need 30 minutes to cross a street connecting one police station to another. All four teams start from Station A at 09:00 hrs. and must return to Station A by 12:00 hrs. They can also pass via Station A at any point on their journeys.
The following facts are known.
1. None of the streets has more than one team traveling along it in any direction at any point in time.
2. Teams 2 and 3 are the only ones in stations E and D respectively at 10:00 hrs.
3. Teams 1 and 3 are the only ones in station E at 10:30 hrs.
4. Teams 1 and 4 are the only ones in stations B and E respectively at 11:30 hrs.
5. Team 1 and Team 4 are the only teams that patrol the street connecting stations A and E.
6. Team 4 never passes through Stations B, D or F.
A, B, C, D, E and F are the six police stations in an area, which are connected by streets as shown below. Four teams – Team 1, Team 2, Team 3 and Team 4 –
patrol these streets continuously between 09:00 hrs. and 12:00 hrs. each day.
The teams need 30 minutes to cross a street connecting one police station to another. All four teams start from Station A at 09:00 hrs. and must return to Station A by 12:00 hrs. They can also pass via Station A at any point on their journeys.
The following facts are known.
1. None of the streets has more than one team traveling along it in any direction at any point in time.
2. Teams 2 and 3 are the only ones in stations E and D respectively at 10:00 hrs.
3. Teams 1 and 3 are the only ones in station E at 10:30 hrs.
4. Teams 1 and 4 are the only ones in stations B and E respectively at 11:30 hrs.
5. Team 1 and Team 4 are the only teams that patrol the street connecting stations A and E.
6. Team 4 never passes through Stations B, D or F.
How many times do the teams pass through Station B in a day?
Question 18.

A, B, C, D, E and F are the six police stations in an area, which are connected by streets as shown below. Four teams – Team 1, Team 2, Team 3 and Team 4 –
patrol these streets continuously between 09:00 hrs. and 12:00 hrs. each day.

The teams need 30 minutes to cross a street connecting one police station to another. All four teams start from Station A at 09:00 hrs. and must return to Station A by 12:00 hrs. They can also pass via Station A at any point on their journeys.
The following facts are known.
1. None of the streets has more than one team traveling along it in any direction at any point in time.
2. Teams 2 and 3 are the only ones in stations E and D respectively at 10:00 hrs.
3. Teams 1 and 3 are the only ones in station E at 10:30 hrs.
4. Teams 1 and 4 are the only ones in stations B and E respectively at 11:30 hrs.
5. Team 1 and Team 4 are the only teams that patrol the street connecting stations A and E.
6. Team 4 never passes through Stations B, D or F.
A, B, C, D, E and F are the six police stations in an area, which are connected by streets as shown below. Four teams – Team 1, Team 2, Team 3 and Team 4 –
patrol these streets continuously between 09:00 hrs. and 12:00 hrs. each day.
The teams need 30 minutes to cross a street connecting one police station to another. All four teams start from Station A at 09:00 hrs. and must return to Station A by 12:00 hrs. They can also pass via Station A at any point on their journeys.
The following facts are known.
1. None of the streets has more than one team traveling along it in any direction at any point in time.
2. Teams 2 and 3 are the only ones in stations E and D respectively at 10:00 hrs.
3. Teams 1 and 3 are the only ones in station E at 10:30 hrs.
4. Teams 1 and 4 are the only ones in stations B and E respectively at 11:30 hrs.
5. Team 1 and Team 4 are the only teams that patrol the street connecting stations A and E.
6. Team 4 never passes through Stations B, D or F.
Which team patrols the street connecting Stations D and E at 10:15 hrs?
Question 19.

A, B, C, D, E and F are the six police stations in an area, which are connected by streets as shown below. Four teams – Team 1, Team 2, Team 3 and Team 4 –
patrol these streets continuously between 09:00 hrs. and 12:00 hrs. each day.

The teams need 30 minutes to cross a street connecting one police station to another. All four teams start from Station A at 09:00 hrs. and must return to Station A by 12:00 hrs. They can also pass via Station A at any point on their journeys.
The following facts are known.
1. None of the streets has more than one team traveling along it in any direction at any point in time.
2. Teams 2 and 3 are the only ones in stations E and D respectively at 10:00 hrs.
3. Teams 1 and 3 are the only ones in station E at 10:30 hrs.
4. Teams 1 and 4 are the only ones in stations B and E respectively at 11:30 hrs.
5. Team 1 and Team 4 are the only teams that patrol the street connecting stations A and E.
6. Team 4 never passes through Stations B, D or F.
A, B, C, D, E and F are the six police stations in an area, which are connected by streets as shown below. Four teams – Team 1, Team 2, Team 3 and Team 4 –
patrol these streets continuously between 09:00 hrs. and 12:00 hrs. each day.
The teams need 30 minutes to cross a street connecting one police station to another. All four teams start from Station A at 09:00 hrs. and must return to Station A by 12:00 hrs. They can also pass via Station A at any point on their journeys.
The following facts are known.
1. None of the streets has more than one team traveling along it in any direction at any point in time.
2. Teams 2 and 3 are the only ones in stations E and D respectively at 10:00 hrs.
3. Teams 1 and 3 are the only ones in station E at 10:30 hrs.
4. Teams 1 and 4 are the only ones in stations B and E respectively at 11:30 hrs.
5. Team 1 and Team 4 are the only teams that patrol the street connecting stations A and E.
6. Team 4 never passes through Stations B, D or F.
How many times does Team 4 pass through Station E in a day?
Question 20.

A, B, C, D, E and F are the six police stations in an area, which are connected by streets as shown below. Four teams – Team 1, Team 2, Team 3 and Team 4 –
patrol these streets continuously between 09:00 hrs. and 12:00 hrs. each day.

The teams need 30 minutes to cross a street connecting one police station to another. All four teams start from Station A at 09:00 hrs. and must return to Station A by 12:00 hrs. They can also pass via Station A at any point on their journeys.
The following facts are known.
1. None of the streets has more than one team traveling along it in any direction at any point in time.
2. Teams 2 and 3 are the only ones in stations E and D respectively at 10:00 hrs.
3. Teams 1 and 3 are the only ones in station E at 10:30 hrs.
4. Teams 1 and 4 are the only ones in stations B and E respectively at 11:30 hrs.
5. Team 1 and Team 4 are the only teams that patrol the street connecting stations A and E.
6. Team 4 never passes through Stations B, D or F.
A, B, C, D, E and F are the six police stations in an area, which are connected by streets as shown below. Four teams – Team 1, Team 2, Team 3 and Team 4 –
patrol these streets continuously between 09:00 hrs. and 12:00 hrs. each day.
The teams need 30 minutes to cross a street connecting one police station to another. All four teams start from Station A at 09:00 hrs. and must return to Station A by 12:00 hrs. They can also pass via Station A at any point on their journeys.
The following facts are known.
1. None of the streets has more than one team traveling along it in any direction at any point in time.
2. Teams 2 and 3 are the only ones in stations E and D respectively at 10:00 hrs.
3. Teams 1 and 3 are the only ones in station E at 10:30 hrs.
4. Teams 1 and 4 are the only ones in stations B and E respectively at 11:30 hrs.
5. Team 1 and Team 4 are the only teams that patrol the street connecting stations A and E.
6. Team 4 never passes through Stations B, D or F.






